from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
X=df.iloc[:, :-1].values
y=df['MEDV'].values
X_train, X_test, y_train, y_test=train_test_split(X, y, test_size=0.3, random_state=0)
slr=LinearRegression()
slr.fit(X_train, y_train)
y_train_pred=slr.predict(X_train)
y_test_pred=slr.predict(X_test)
잔차 그래프(residual plot)
모델의 특성이 많기 때문에 2차원 그래프로 선형 회귀 직성(초평면, hyperplane)을 그릴 수 없다.
대신 예측값에 대한 잔차 그래프인 잔차 그래프(residual plot)를 사용
plt.scatter(y_train_pred, y_train_pred-y_train, c='steelblue', marker='o', edgecolor='white', label='Training data')
plt.scatter(y_test_pred, y_test_pred-y_test, c='limegreen', marker='s', edgecolor='white', label='Test data')
plt.xlabel('Predicted Values')
plt.ylabel('Residuals')
plt.legend(loc='upper left')
plt.hlines(y=0, xmin=-10, xmax=50, color='black', lw=2)
plt.xlim([-10, 50])
plt.tight_layout()
plt.show()

좋은 회귀 모델은 오차가 랜덤하게 분포되고, 잔차는 중앙선 주변으로 랜덤하게 흩어져야 한다.
평균 제곱 오차(Mean Squared Error, MSE)
MSE는 선형 회귀 모델을 훈련하기 위해 최소화하는 제곱 오차합(SSE)의 평균이다.
from sklearn.metrics import mean_squared_error
print('훈련 MSE: %.3f, 테스트 MSE: %.3f' %(mean_squared_error(y_train, y_train_pred), mean_squared_error(y_test, y_test_pred)))
훈련 MSE: 19.958, 테스트 MSE: 27.196
훈련 데이터셋 MSE보다 테스트 데이터셋 MSE가 훨씬 크다. 이는 과대적합 되었음을 말해 준다.
하지만 분류 정확도와 달리 MSE는 단위에 따라 큰 차이가 발생한다.
따라서 결정 계수(Coefficient of determination, R^2)가 더 유용할 수 있다.
결정 계수는 MSE의 표준화 버전으로 생각할 수 있다.(타깃의 분산에서 모델이 잡아낸 비율)
결정 계수
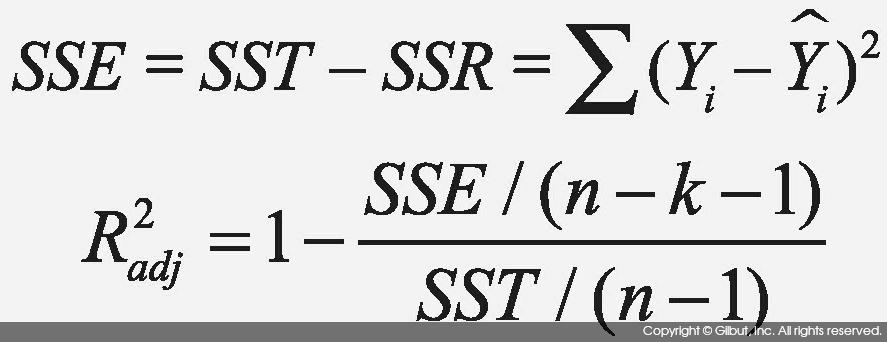

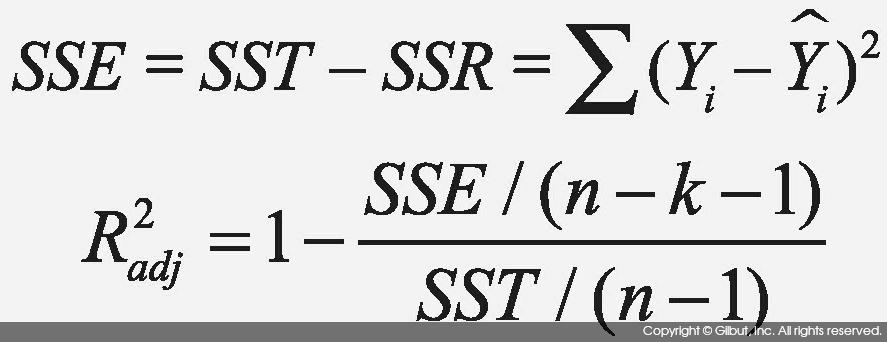
SSE는 오차 제곱합
SST는 전체 제곱합(Total Sum of Squares)
위 식을 정리하면
R^2=1- { MSE/ Var(y) }
R^2은 훈련 데이터 셋에서 0-1 사이의 값을 가지며, 테스트 데이터 셋에서는 음수가 될 수 있따.
R^2=1이면 MSE=0이고 모델이 데이터를 완벽히 학습한 것이다.
from sklearn.metrics import r2_score
print('훈련 R^2: %.3f, 테스트 R^2: %.3f' %(r2_score(y_train, y_train_pred), r2_score(y_test, y_test_pred)))
훈련 R^2: 0.765, 테스트 R^2: 0.673